The entire world runs on electricity and we often take it for granted. But as soon as a blackout strikes out of the blue, we find ourselves pretty much obstructed and unable to use anything.
Contents
Whatever gadget, gizmo, or hardware we have, it depends on electricity one way or the other. Even if it does not use electricity, it was almost certainly built using electrical power. Electricity appears to be a perplexing mysterious force that magically operates many things we are using.
But you will be surprised to know that electricity is not all that hard to understand. You can get started with a simple electrical circuit to learn how electricity works. This will give you a much better understanding of the world around you.
Simply put: in a closed circuit, electrons will be transported through the wires from a power source (battery), into a resistor (light bulb). At the moment the bulb receives enough electrons, the bulb will light up.
Did you know that the most fun way to learn about electricity is to experiment? Here is how to build an electric circuit.
Before you start, you should gather all the materials and tools needed to build a circuit. Also, make sure that you do everything under the supervision of an adult who knows about electricity.

Materials and Tools Needed to Build An Electric Circuit
Here are the components, materials, and tools needed to build a simple electric circuit.
- Insulated wires
- Battery (aka your power source)
- Battery pack
- Bulb (aka your resistor)
- Light bulb holder
- Electrical tape
- Wire Stripper or scissor
You can get a small light bulb that is between 1 to 2 volts. Small miniature bulbs are good enough for a simple electric circuit.

How To Build An Electric Circuit
Step 1
You will have to strip the wires to expose both ends of the wires. Once the wire ends are exposed, you can connect both wires to join the battery on one side and to the bulb on the other side. Wire strippers will help you to do the job. Just remove the insulation using the wire stripper. For both wires, remove around an inch of insulation from both ends. Scissors may also work if you do not have a wire stripper. But be careful not to cut wires all the way through.

Step 2
You will now have to place batteries inside the battery pack. This will provide the electric power for lighting up the bulb. If you only use one battery, you may skip this step. Make sure to connect the batteries right. Check the polarities shown in the power pack. Put the positive battery side at the positive terminal marked ‘+’ in the power source terminal. The negative battery side will then go towards the ‘-’ side of the power pack. This is the right orientation.
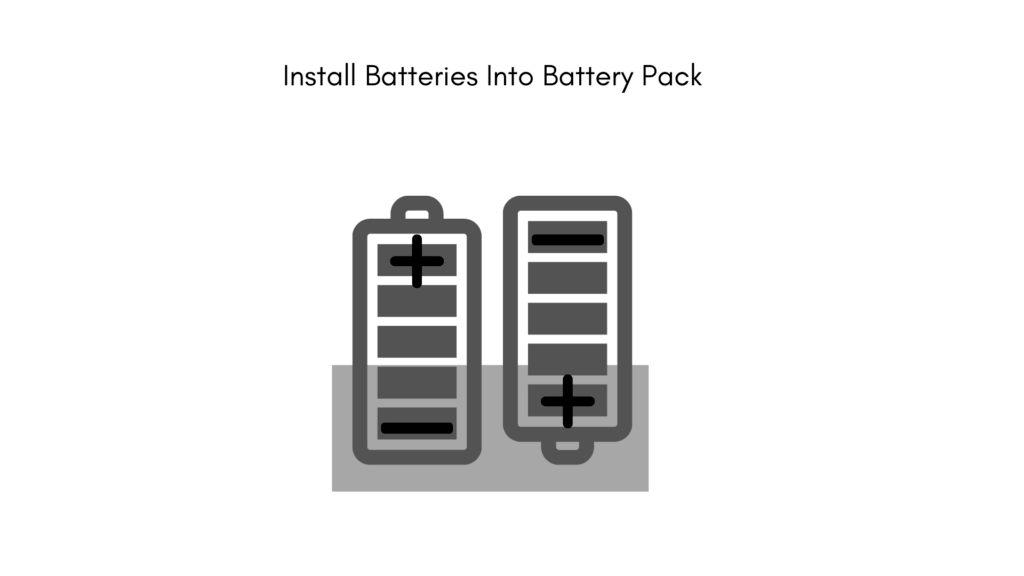
Step 3
You will now have to connect the bare ends of the wires with the power pack. Wires will provide a path for electrons and allow them to flow. Connect the wires using electrical tape. Make sure that the exposed metal of the wire is in contact with the battery pack terminal, otherwise, the circuit will not work. Avoid touching the wire with your bare hands while connecting it to the battery pack. You might get a small shock if you are not careful.
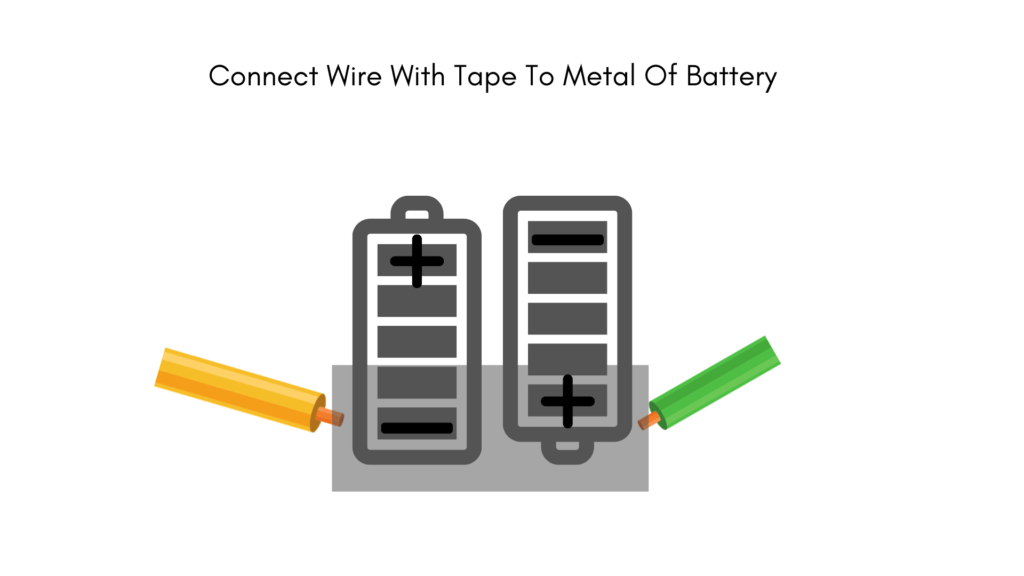
Step 4
After connecting the wires to the battery pack, you can now connect the other ends of the wires to the bulb holder. Loosen the battery pack screws so that there is enough space to pass the exposed wire ends through this opening. Once you pass exposed wires through the gap, tighten the screws so that there is strong physical contact between the wires and the battery pack.
Step 5
Now screw the bulb in place on the bulb holder. Once in the right position, the bulb will light up. In case the bulb does not light up, check the wire ends for loose connections. Tighten these connections for strong contact that will allow electricity to flow freely.

How Does An Electric Circuit Work Exactly?
An electric circuit is simply a path through which electricity can flow. Think of an electric circuit as a pipe network for flowing water. This simple analogy can give you a much better understanding of electrical concepts, especially voltage and amperes.
The wires are akin to water pipes. Wires help electrons flow just like pipes provide a path for flowing water.
The battery in the circuit is like a water pump. Just like water cannot start flowing without a pump or some other force to drive it through pipes, electrons cannot flow unless they get their energy from a power source like a battery.
The Function Of A Switch Between Battery And Bulb
If you add a switch between the battery pack and the bulb, you are able to open and close the circuit as you please. When you open the switch, you will get an open circuit. This simply means that there is an air gap through which electrons cannot flow. Because electrons will not flow with an open circuit, the circuit will not work. When you close the switch, the circuit will close and become complete. Electrons can now flow so that the circuit works. A lamp switch works the same way: once you flip it, the lamp will switch on or off.
What Is Electricity?
Two very important measures in electric circuits are volts and amperes. Here is what they imply.
Volts
Just like a water pump pressurizes water to make it flow, the battery or power source ‘pressurizes’ electrons. It gives energy to electrons and this energy is measured in volts. Simply put, voltage is the energy possessed by a unit amount of electrons.
To make it simpler, just think of volts as ‘power’ given to electrons by the battery.
But then, what does ‘15 volts’ on a bulb mean? Is the bulb giving 15 volts of ‘power’ to the electrons?
No. The bulb needs to consume 15 volts of power to work properly. Thus, the battery pack provides 15 volts ‘power’ to the electrons. The electrons transfer this ‘power’ to the bulb so that it works.
Amperes
Amperes is a measure of electron flow. This is almost like volume flowrate for water which can be measured, for instance, in cubic feet per second.
Summary
So there you have it. If you can imagine that your battery is like a pump, wires are like water pipes and electrons are like water, you can get a pretty decent idea of how an electric circuit works. In a closed circuit, electrons will be transported through the wires from a power source (battery), into a resistor (light bulb). At the moment the bulb receives enough electrons, the bulb will light up. When you place a switch between the battery and bulb, you are able to ‘open’ and ‘close’ your electric circuit.
As a parent of a five-year-old inquisitive boy, I have gained a lot of experience finding fun activities and toys to help him understand science and understanding our world in general. On this blog, you’ll find an extensive amount of tutorials, guides, and toys about Science, Technology, Engineering, and Math based on my personal experience to help your child develop critical STEM skills.






